STATISTICS-session 5 and 6

Probability  is a measure or estimation of how likely it is that something will happen or that a statement is true. Probabilities are given a value between 0 (0% chance or will not happen) and 1 (100% chance or will happen).
According to Richard Jeffrey, "Before the middle of the seventeenth century, the term 'probable' (Latin probabilis) meant approvable, and was applied in that sense, univocally, to opinion and to action. A probable action or opinion was one such as sensible people would undertake or hold, in the circumstances.

Different probabability approaches:
There are three main approaches for probability.They are:

1.A Priori:This type of approach is carried on when we have prior information of the data.
Priori probabilities are most often used within the deduction method of calculating probability. This is because you must use logic to determine what outcomes of an event are possible in order to determine the number of ways these outcomes can occur. 
Example:consider how the price of a share can change. Its price can increase, decrease or remain the same. Therefore, according to a priori probability, we can assume that there is a 1-in-3, or 33%, chance of one of the outcomes occurring (all else remaining equal).

2.Empirical approach:This type of approach is carried out when the information is collected.
Example:Data collected from the students and which is stored in the database.

3.Subjective approach:A probability derived from an individual's personal judgment about whether a specific outcome is likely to occur. Subjective probabilities contain no formal calculations and only reflect the subject's opinions and past experience.
Example: Believing that the probability that the sales of dove soap will go up tomorrow is 60%, then to be consistent we  cannot believe that the probability that the Dove soap will be  down tomorrow is also 60%.

Venn diagrams:diagramatic representation of relations between two or more events

Sample Space:All possible outcomes of an event or an experiment

Mutually Exclusive Events:Two events are 'mutually exclusive' if they cannot occur at the same time.
Example : tossing a coin once, which can result in either heads or tails, but not both.


Independent Events:Independent Events are not affected by previous events.
Example:When we toss a coin three times each time the probability of getting a head is 0.5

LAWS OF PROBABILITY:There are mainly three laws in probability.They are

1.ADDITION LAW:probability that A or B will happen is the sum of the probabilities that A will happen and B will happen.

2.CONDITIONAL LAW:It is the probability that an event will occur, when another event is known to occur or to have occurred. If the events are A and B respectively, this is said to be "the probability of A given B".

3.MULTIPLICATION LAW:If X and Y are two independent events with probabilities P(X) and P(Y) respectively, then the probability that X and Y will both happen is found by multiplying the two probabilities together.

BAYES THEOREM:It allows us to calculate the conditional probability one way(e.g.P(B/A)) when we know the conditional probability the other way(e.g.P(A/B))

Summary of probabilities

Event	Probability
A
not A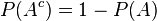
A or B
A and B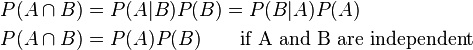
A given B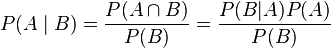

P.PRIYATHAM KIREETI(2013183)

PRIYADARSHI TANDON(2013211)

P.KALYANI(2013184)

NISHIDH LAD(2013176)

P.S.V.P.S.G.KARTHEEKI(2013198)