SAMPLING:
A process used in statistical analysis in which a predetermined number of observations will be taken from a larger population. The methodology used to sample from a larger population will depend on the type of analysis being performed, but will include simple random sampling, systematic sampling and observational sampling.
The sample should be a representation of the general population.When taking a sample from a larger population, it is important to consider how the sample will be drawn. To get a representative sample, the sample must be drawn randomly and encompass the entire population. For example, a lottery system could be used to determine the average age of students in a University by sampling 10% of the student body, taking an equal number of students from each faculty.
The sampling process comprises several stages:
- Defining the population of concern
- Specifying a sampling frame, a set of items or events possible to measure
- Specifying a sampling method for selecting items or events from the frame
- Determining the sample size
- Implementing the sampling plan
- Sampling and data collecting
- Data which can be selected
1)Probability Sampling:
A probability sampling method is any method of sampling that utilizes some form of random selection. In order to have a random selection method, you must set up some process or procedure that assures that the different units in your population have equal probabilities of being chosen. Humans have long practiced various forms of random selection, such as picking a name out of a hat, or choosing the short straw. These days, we tend to use computers as the mechanism for generating random numbers as the basis for random selection
Example: We want to estimate the total income of adults living in a given street. We visit each household in that street, identify all adults living there, and randomly select one adult from each household. (For example, we can allocate each person a random number, generated from a uniform distribution between 0 and 1, and select the person with the highest number in each household). We then interview the selected person and find their income. People living on their own are certain to be selected, so we simply add their income to our estimate of the total. But a person living in a household of two adults has only a one-in-two chance of selection. To reflect this, when we come to such a household, we would count the selected person's income twice towards the total. (The person who is selected from that household can be loosely viewed as also representing the person who isn't selected.)
In the above example, not everybody has the same probability of selection; what makes it a probability sample is the fact that each person's probability is known. When every element in the population does have the same probability of selection, this is known as an 'equal probability of selection' (EPS) design. Such designs are also referred to as 'self-weighting' because all sampled units are given the same weight.
Probability sampling includes:simple random sampling ,systematic sampling. Probability Proportional to Size Sampling, and cluster or multistage sampling These various ways of probability sampling have two things in common:
- Every element has a known nonzero probability of being sampled and
- involves random selection at some point
2)Non-probability sampling:
It is any sampling method where some elements of the population have no chance of selection, or where the probability of selection can't be accurately determined. It involves the selection of elements based on assumptions regarding the population of interest, which forms the criteria for selection. Hence, because the selection of elements is nonrandom, non probability sampling does not allow the estimation of sampling errors. These conditions give rise to exclusion bias, placing limits on how much information a sample can provide about the population. Information about the relationship between sample and population is limited, making it difficult to extrapolate from the sample to the population.
Example: We visit every household in a given street, and interview the first person to answer the door. In any household with more than one occupant, this is a non probability sample, because some people are more likely to answer the door (e.g. an unemployed person who spends most of their time at home is more likely to answer than an employed housemate who might be at work when the interviewer calls) and it's not practical to calculate these probabilities.
Non probability sampling methods include accidential samplings,quota samplings and purposive sampling. In addition, non response effects may turn any probability design into a non probability design if the characteristics of non response are not well understood, since non response effectively modifies each element's probability of being sampled.
SAMPLING METHODS:
1)CLUSTER SAMPLING:
Cluster sampling may be used when it is either impossible or impractical to compile an exhaustive list of the elements that make up the target population. Usually, however, the population elements are already grouped into sub populations and lists of those sub populations already exist or can be created. For example, let’s say the target population in a study was church members in the United States. There is no list of all church members in the country. The researcher could, however, create a list of churches in the United States, choose a sample of churches, and then obtain lists of members from those churches.
One stage cluster sample:
When a researcher includes all of the subjects from the chosen clusters into the final sample, this is called a one-stage cluster sample.
Two stage cluster sample:
A two-stage cluster sample is obtained when the researcher only selects a number of subjects from each cluster – either through simple random sampling or systematic random sampling.
Advantages of Cluster Sampling-
One advantage of cluster sampling is that it is cheap, quick, and easy. Instead of sampling the entire country when using simple random sampling, the research can instead allocate resources to the few randomly selected clusters when using cluster sampling.
A second advantage to cluster sampling is that the researcher can have a larger sample size than if he or she was using simple random sampling. Because the researcher will only have to take the sample from a number of clusters, he or she can select more subjects since they are more accessible.
Disadvantages of Cluster Sampling-
One main disadvantage of cluster sampling is that is the least representative of the population out of all the types of probability samples. It is common for individuals within a cluster to have similar characteristics, so when a researcher uses cluster sampling, there is a chance that he or she could have an over represented or underrepresented cluster in terms of certain characteristics. This can skew the results of the study.
In cluster sampling, we follow these steps:
- divide population into clusters (usually along geographic boundaries)
- randomly sample clusters
- measure all units within sampled clusters
2)SYSTEMATIC SAMPLING:
A common way of selecting members for a sample population using systematic sampling is simply to divide the total number of units in the general population by the desired number of units for the sample population. The result of the division serves as the marker for selecting sample units from within the general population.
In a systematic sample, the elements of the population are put into a list and then every k th element in the list is chosen (systematically) for inclusion in the sample. For example, if the population of study contained 2,000 students at a high school and the researcher wanted a sample of 100 students, the students would be put into list form and then every 20th student would be selected for inclusion in the sample. To ensure against any possible human bias in this method, the researcher should select the first individual at random. This is technically called a systematic sample with a random start.
For example, if you wanted to select a random group of 1,000 people from a population of 50,000 using systematic sampling, you would simply select every 50th person, since 50,000/1,000 = 50.
Systematic sampling also begins with the complete sampling frame and assignment of unique identification numbers. However, in systematic sampling, subjects are selected at fixed intervals, e.g., every third or every fifth person is selected. The spacing or interval between selections is determined by the ratio of the population size to the sample size (N/n). For example, if the population size is N=1,000 and a sample size of n=100 is desired, then the sampling interval is 1,000/100 = 10, so every tenth person is selected into the sample. The selection process begins by selecting the first person at random from the first ten subjects in the sampling frame using a random number table; then 10th subject is selected.
If the desired sample size is n=175, then the sampling fraction is 1,000/175 = 5.7, so we round this down to five and take every fifth person. Once the first person is selected at random, every fifth person is selected from that point on through the end of the list.
With systematic sampling like this, it is possible to obtain non-representative samples if there is a systematic arrangement of individuals in the population. For example, suppose that the population of interest consisted of married couples and that the sampling frame was set up to list each husband and then his wife. Selecting every tenth person (or any even-numbered multiple) would result in selecting all males or females depending on the starting point. This is an extreme example, but one should consider all potential sources of systematic bias in the sampling process
3)Multi-Stage Sampling:
The four methods we've covered so far -- simple, stratified, systematic and cluster -- are the simplest random sampling strategies. In most real applied social research, we would use sampling methods that are considerably more complex than these simple variations. The most important principle here is that we can combine the simple methods described earlier in a variety of useful ways that help us address our sampling needs in the most efficient and effective manner possible. When we combine sampling methods, we call this multi-stage sampling.
For example, consider the idea of sampling New York State residents for face-to-face interviews. Clearly we would want to do some type of cluster sampling as the first stage of the process. We might sample townships or census tracts throughout the state. But in cluster sampling we would then go on to measure everyone in the clusters we select. Even if we are sampling census tracts we may not be able to measure everyone who is in the census tract. So, we might set up a stratified sampling process within the clusters. In this case, we would have a two-stage sampling process with stratified samples within cluster samples. Or, consider the problem of sampling students in grade schools. We might begin with a national sample of school districts stratified by economics and educational level. Within selected districts, we might do a simple random sample of schools. Within schools, we might do a simple random sample of classes or grades. And, within classes, we might even do a simple random sample of students. In this case, we have three or four stages in the sampling process and we use both stratified and simple random sampling. By combining different sampling methods we are able to achieve a rich variety of probabilistic sampling methods that can be used in a wide range of social research contexts
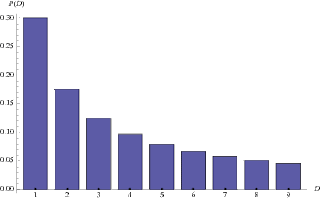
BENFORD'S LAW:
A phenomenological law also called the first digit law, first digit phenomenon, or leading digit phenomenon. Benford's law states that in listings, tables of statistics, etc., the DIGIT 1 tends to occur with probability  , much greater than the expected 11.1% (i.e., one digit out of 9). Benford's law can be observed, for instance, by examining tables of logarithms and noting that the first pages are much more worn and smudged than later pages . While Benford's law unquestionably applies to many situations in the real world, a satisfactory explanation has been given only recently through the work of Hill (1998).
, much greater than the expected 11.1% (i.e., one digit out of 9). Benford's law can be observed, for instance, by examining tables of logarithms and noting that the first pages are much more worn and smudged than later pages . While Benford's law unquestionably applies to many situations in the real world, a satisfactory explanation has been given only recently through the work of Hill (1998).
Benford's law applies to data that are not dimensionless, so the numerical values of the data depend on the units. If there exists a universal probability distribution  over such numbers, then it must be invariant under a change of scale, so
over such numbers, then it must be invariant under a change of scale, so
(1)
|
If  , then
, then  , and normalization implies
, and normalization implies  . Differentiating with respect to
. Differentiating with respect to  and setting
and setting  gives
gives
(2)
|
having solution  . Although this is not a proper probability distribution (since it diverges), both the laws of physics and human convention impose cutoffs. For example, randomly selected street addresses obey something close to Benford's law.
. Although this is not a proper probability distribution (since it diverges), both the laws of physics and human convention impose cutoffs. For example, randomly selected street addresses obey something close to Benford's law.
Benford's law applies not only to scale-invariant data, but also to numbers chosen from a variety of different sources. Explaining this fact requires a more rigorous investigation of central limit like theorems for the mantissas of random variables under multiplication As the number of variables increases, the density function approaches that of the above logarithmic distribution.
Written By:
Poorva Saboo (2013200)
Group members:
Poorva saboo
Abhishek panwala
Pareena Neema
Parita Mandhana
Raghav Kabra
No comments:
Post a Comment